Identitas Trigonometri dan Rumus rumusnya

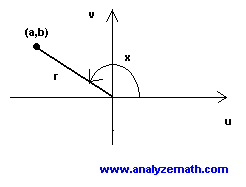
Below are some of the most important definitions, identities and formulas in trigonometry. 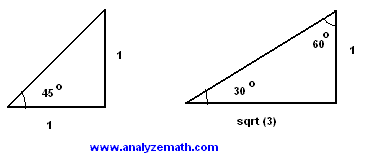Trigonometric Functions of Acute Angles sin X = opp / hyp = a / c , csc X = hyp / opp = c / a tan X = opp / adj = a / b , cot X = adj / opp = b / a cos X = adj / hyp = b / c , sec X = hyp / adj = c / b , Trigonometric Functions of Arbitrary Angles sin X = b / r , csc X = r / b tan X = b / a , cot X = a / b cos X = a / r , sec X = r / a Special Triangles Special triangles may be used to find trigonometric functions of special angles: 30, 45 and 60 degress. Sine and Cosine Laws in Triangles In any triangle we have: 1 - The sine law sin A / a = sin B / b = sin C / c 2 - The cosine laws a 2 = b 2 + c 2 - 2 b c cos A b 2 = a 2 + c 2 - 2 a c cos B c 2 = a 2 + b 2 - 2 a b cos C Relations Between Trigonometric Functions cscX = 1 / sinX sinX = 1 / cscX secX = 1 / cosX cosX = 1 / secX tanX = 1 / cotX cotX = 1 / tanX tanX = sinX / cosX cotX = cosX / sinX Pythagorean Identities sin 2X + cos 2X = 1 1 + tan 2X = sec 2X 1 + cot 2X = csc 2X Negative Angle Identities sin(-X) = - sinX , odd function csc(-X) = - cscX , odd function cos(-X) = cosX , even function sec(-X) = secX , even function tan(-X) = - tanX , odd function cot(-X) = - cotX , odd function Cofunctions Identities sin(pi/2 - X) = cosX cos(pi/2 - X) = sinX tan(pi/2 - X) = cotX cot(pi/2 - X) = tanX sec(pi/2 - X) = cscX csc(pi/2 - X) = secX Addition Formulas cos(X + Y) = cosX cosY - sinX sinY cos(X - Y) = cosX cosY + sinX sinY sin(X + Y) = sinX cosY + cosX sinY sin(X - Y) = sinX cosY - cosX sinY tan(X + Y) = [ tanX + tanY ] / [ 1 - tanX tanY] tan(X - Y) = [ tanX - tanY ] / [ 1 + tanX tanY] cot(X + Y) = [ cotX cotY - 1 ] / [ cotX + cotY] cot(X - Y) = [ cotX cotY + 1 ] / [ cotX - cotY] Sum to Product Formulas cosX + cosY = 2cos[ (X + Y) / 2 ] cos[ (X - Y) / 2 ] sinX + sinY = 2sin[ (X + Y) / 2 ] cos[ (X - Y) / 2 ] Difference to Product Formulas cosX - cosY = - 2sin[ (X + Y) / 2 ] sin[ (X - Y) / 2 ] sinX - sinY = 2cos[ (X + Y) / 2 ] sin[ (X - Y) / 2 ] Product to Sum/Difference Formulas cosX cosY = (1/2) [ cos (X - Y) + cos (X + Y) ] sinX cosY = (1/2) [ sin (X + Y) + sin (X - Y) ] cosX sinY = (1/2) [ sin (X + Y) - sin[ (X - Y) ] sinX sinY = (1/2) [ cos (X - Y) - cos (X + Y) ] Difference of Squares Formulas sin 2X - sin 2Y = sin(X + Y)sin(X - Y) cos 2X - cos 2Y = - sin(X + Y)sin(X - Y) cos 2X - sin 2Y = cos(X + Y)cos(X - Y) Double Angle Formulas sin(2X) = 2 sinX cosX cos(2X) = 1 - 2sin 2X = 2cos 2X - 1 tan(2X) = 2tanX / [ 1 - tan 2X ] Multiple Angle Formulas sin(3X) = 3sinX - 4sin 3X cos(3X) = 4cos 3X - 3cosX sin(4X) = 4sinXcosX - 8sin 3XcosX cos(4X) = 8cos 4X - 8cos 2X + 1 Half Angle Formulas sin (X/2) = + or - SQRT [ (1 - cosX) / 2 ] cos (X/2) = + or - SQRT [ (1 + cosX) / 2 ] tan (X/2) = + or - SQRT [ (1 - cosX) / (1 + cosX) ] = sinX / (1 + cosX) = (1 - cosX) / sinX Power Reducing Formulas sin 2X = 1/2 - (1/2)cos(2X)) cos 2X = 1/2 + (1/2)cos(2X)) sin 3X = (3/4)sinX - (1/4)sin(3X) cos 3X = (3/4)cosX + (1/4)cos(3X) sin 4X = (3/8) - (1/2)cos(2X) + (1/8)cos(4X) cos 4X = (3/8) + (1/2)cos(2X) + (1/8)cos(4X) sin 5X = (5/8)sinX - (5/16)sin(3X) + (1/16)sin(5X) cos 5X = (5/8)cosX + (5/16)cos(3X) + (1/16)cos(5X) sin 6X = 5/16 - (15/32)cos(2X) + (6/32)cos(4X) - (1/32)cos(6X) cos 6X = 5/16 + (15/32)cos(2X) + (6/32)cos(4X) + (1/32)cos(6X) Trigonometric Functions Periodicity sin (X + 2Pi) = sin X , period 2Pi cos (X + 2Pi) = cos X , period 2Pi sec (X + 2Pi) = sec X , period 2Pi csc (X + 2Pi) = csc X , period 2Pi tan (X + Pi) = tan X , period Pi cot (X + Pi) = cot X , period Pi Sumber : http://www.analyzemath.com